Ecuaciones lineales. Introducción
Para iniciar el estudio de las ecuaciones lineales conviene conocer el concepto de igualdad. Una igualdad es la afirmación de que dos cosas o entes matemáticos son iguales. Ejemplos de igualdades son las expresiones,
\(\textcolor{#ff0080}{1.}~~F=ma~~~~\textcolor{#ff0080}{2.}~~ x+3=7~~~~\textcolor{#ff0080}{3.}~~d=vt~~~~\textcolor{#ff0080}{4.}~~A=wl\).
Los elementos de una igualdad son las incógnitas y las constantes, agrupadas en dos miembros, por ejemplo:
\({\underbrace{8x+3}_{primer~miembro}}= {\underbrace{5+x}_{segundo~miembro}}\) donde \(x\) es llamada incógnita.
Las incógnitas representan valores desconocidos, mientras que las constantes representan valores conocidos.
Concepto de identidad: una identidad es una igualdad que se cumple para todo valor dentro del dominio de la variable.
Por ejemplos:
\(\textcolor{#ff0080}{1.}~~\left(w-x\right)\left(w+x\right)\equiv\ w^2-x^2\) (producto de binomios conjugados).
\(\textcolor{#ff0080}{2.}~~\left(w-x\right)^2\equiv w^2-2wx+x^2\) (cuadrado de un binomio).
Son identidades porque se verifican para todos los valores de las variables. Donde el símbolo \(\equiv\) se lee "idéntico a" o "equivalente a".
Concepto de ecuación.
Una ecuación es una igualdad que se cumple para ciertos valores de la incógnita. Note la diferencia entre identidad y ecuación, las identidades se cumplen para todo valor, mientras que las ecuaciones para ciertos valores.
Grado de una ecuación.
El grado de una ecuación es el mayor exponente de la variable en la ecuación.
Por ejemplo, \(y=mx+n\) es de \(1^{er}\) grado, mientras que \(A=\pi r^2\) es de \(2^{do}\) grado para \(r\).
En la expresión para el volumen de una esfera \(V=\frac{4}{3}\pi r^3\) es de \(1^{er}\) para \(V\), pero de \(3^{er}\) grado para \(r\).
La ecuación de posición \(d=\frac{1}{2}at^2+vt+d_0\) es de segundo grado para \(t\) y de primer grado para todas las demás
Si una ecuación es de primer grado se le llama "ecuación lineal", si es de segundo grado se le llama “ecuación cuadrática” si es de tercer grado “ecuación cúbica” y así sucesivamente.
Axioma de las igualdades.
El axioma de las igualdades expresa que si en una igualdad se realiza la misma operación en ambos miembros, la igualdad se mantiene. Recuerde esta afirmación, la va a necesitar una y otra vez.
Raices o ceros
Las raíces o ceros de una ecuación son los valores de la variable que la hacen verdadera. Por el teorema fundamental del álgebra una ecuación de grado \(n\), tiene \(n\) raíces.
Resolver una ecuación es determinar sus raíces.
Desde curso y grados anteriores ya se ha trabajado en la resolución de ecuaciones, al dar solución a situaciones geométricas como áreas y perímetros o al trabajar con la más famosa de todas las ecuaciones, teorema de Pitágoras \(r^2=x^2+y^2\).
Resolviendo ecuaciones lineales.
Como ya se ha dicho a una ecuación de primer grado se le llama "ecuación lineal". La forma más simple para ella es del tipo \(x=n\), donde \(x\) es la variable y \(n\) es un número cualquiera, su característica principal es que su gráfica es una línea recta y de esto es el nombre de lineal.
Resolver una ecuación lineal es encontrar su raíz o cero (valor que la hace verdadera), y por el teorema fundamental del álgebra, ésta raíz es única.
Imagine que por ejemplo se tiene la ecuación \(x+7=12\) ahora piense ¿Cuánto debe valer \(x\) para que la afirmación \(x+7=12\) sea verdadera? Desde luego que la respuesta es \(x=5\) ya que \(5+7=12\). Sin embargo, no siempre es tan fácil determinar la raíz de una ecuación, algunas veces es necesario un poco más de rigor matemático para ello.
¿Cómo resolver una ecuación?
Al resolver ecuaciones, tenga en cuenta siempre:
1. Simplificar y resolver las operaciones planteadas, siguiendo siempre el orden operacional.
2. Si hay fracciones, multiplicar toda la expresión por el mínimo común denominador m.c.ds. simplificará la expresión. ¡Trabajar con enteros es más fácil que con fracciones!
3. Despejar la incógnita aplicando el axioma de las ecuaciones al realizar la misma operación en ambos miembros. Comience por separar términos escribiendo en un miembro todas las incógnitas y en el otro todas las constantes, realice operaciones indicadas y si es necesario vuelva a aplicar el axioma hasta que la incógnita esté totalmente despejada (coeficiente igual a uno y su valor simplificado).
Ejemplo 1. Resolver \(3(x+5)=24\) \begin{array}{l l} 3(x+5)=24&{\rm Ecuación~dada.}\\ 3x+15=24&{\rm Multiplicando}\\ 3x+15-15=24-15&{\rm Restando~15}\\ 3x=9&{\rm Simplificando}\\ \frac{3x}{3}=\frac93&{\rm Dividiendo~por~3}\\ x=3&{\rm Simplificando} \end{array} Ejemplo 2. Resolver \(4(x-9)=12(-3)\) \begin{align} &4(x-9)=12(-3)~~~~~~~~~~~~~~~~~\mathrm{Ecuación~dada.}\\ &4x-36=-36~~~~~~~~~~~~~~~~~~~~~~~\mathrm{Multiplicando}\\ &4x-36+36=-36+36~~~~~\mathrm{Sumando~36}\\ &4x=0~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\mathrm{Simplificando}\\ &\frac{4x}4=\frac04~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\mathrm{Dividiendo~por~} 4\\ &x=0~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\mathrm{Simplificando} \end{align} Ejemplo 3. Resolver \(7(2x-5)=8(3x-4)\) \begin{align} &7(2x-5)=8(3x-4)~~~~~~~~~~~~~~~~~~~~\mathrm{Ecuación~dada.}\\ &14x-35=24x-32~~~~~~~~~~~~~~~~~~~~~~\mathrm{Multiplicando}\\ &14x-35+35=24x-32+35~~~~\mathrm{Sumando~35}\\ &14x=24x+3~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\mathrm{Simplificando}\\ &14x-24x=24x+3-24x~~~~~~~~~~~\mathrm{Restando~}24x\\ &-10x=3~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\mathrm{Simplificando}\\ &\frac{-10x}{-10}=\frac3{-10} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \mathrm{Dividiendo~por~-10}\\ &x=-\frac3{10}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\mathrm{Simplificando} \end{align}
Trasposición de términos.
Trasponer un ente matemático, es escribir dicho ente en un miembro diferente del que ocupa en una igualdad.
En el ejemplo 1 al escribir \(3x+15=24\) para despejar \(x\) se escribe \(3x+15-15=24-15\), de donde \(3x=9\).
Se debe notar lo que ha pasado con el \(15\), estaba sumando en el lado derecho y ahora aparece restando en el lado izquierdo. Esta acción en una igualdad recibe el nombre de trasposición de términos, es decir, si en una igualdad una cantidad está en un miembro bajo la acción de una operación aritmética, dicha cantidad “pasa al otro lado” bajo la acción de la operación contraria a la que estaba.
En el ejemplo 2 se tiene \(4x-36=-36\) y en el siguiente paso se luego se escribe \(4x-36+36=-36+36\), al simplificar el lado izquierdo se tiene \(4x=-36+36\) y abusando del lenguaje se dice "\(36\) estaba restando en el lado izquierdo pasa sumando al lado derecho".
Procure comprender la expresión "pasa al otro lado", los números no tiene piernas para poder pasar de un lado a otro. La trasposición se realiza para agrupar en un solo miembro las variables y en el otro las constantes aplicando el axioma de las igualdades. De aquí en adelante al resolver los ejercicios se hará la trasposición de términos con la finalidad de ahorrar escritura.
Ejemplo 4. Resolver \(5\left(x+3\right)^2=5x\left(x+13\right)\) \begin{align} &5(x+3)^2=5x(x+13)~~~~~~~~~~~~~~~~ \mathrm{Ecuación~dada.}\\ &5(x^2+6x+9)=5x(x+13)~~~~~~\mathrm{Desarrollando~potencia}\\ &5x^2+30x+45=5x^2+65x~~~~~~~\mathrm{Multiplicando}\\ &5x^2+30x-5x^2-65x=-45~~~~\mathrm{Trasposición}\\ &-35x=-45~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \mathrm{Simplificando}\\ &x=\frac{-45}{-35} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ {\rm Despejando~}x\\ &x=\frac97~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ {\rm Simplificando} \end{align} Ejemplo 5. Coeficientes fraccionarios. Resolver, $$\frac{2}{3}x+\frac{5}{7}x=58$$ Solución: comience por multiplicar toda la expresión por el mínimo común denominador \(m.c.ds.\) (mínimo común múltiplo de los denominadores) para así simplificar los denominadores y luego realice la operaciones. \begin{align} &21\left(\frac{2}{3}x+\frac{5}{7}x\right)=21(58)~~~~~21 ~{\rm es}~ m.c.ds.\\ &14x+15x=1218~~~~~~~~~~{\rm Multiplicando}\\ &29x=1218~~~~~~~~~~~~~~~~~~~{\rm Simplificando}\\ &x=\frac{1218}{29}~~~~~~~~~~~~~~~~~~~~~{\rm Despejando}~x\\ &x=42~~~~~~~~~~~~~~~~~~~~~~~~~~~{\rm Simplificando} \end{align} Ejemplo 6. Coeficientes fraccionarios. Resolver, $$\frac{5}{3}x+\frac{7}{16}x=\frac{5}{9}x$$ Solución: proceda igual que en el ejemplo anterior multiplicando toda la expresión por el mínimo común denominador \(m.c.ds.\) para simplificar los denominadores y luego realice las operaciones. \begin{align} &144\left(\frac{5}{3}x+\frac{7}{16}x\right)=144\left(\frac{5}{9}x\right)~~~~~144~\mathrm{es}~m.c.ds.\\ &240x+63x=80x~~~~~~~~~~~~~~~~~{\rm Multiplicando}\\ &240x+63x-80x=0~~~~~~~~~~{\rm Trasposición.}\\ &223x=0~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \mathrm{Simplificando}\\ &x=\frac0{223}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ {\rm Despejando}~x\\ &x=0~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ {\rm Simplificando} \end{align} Ejemplo 7. Un resultado que no existe. Resolver \(7(x-4)=7x+12\). \begin{align} &7x-28=7x+12~~~~~~~\mathrm{Multiplicando}\\ &7x-7x=12+28~~~~~~~\mathrm{Trasposición}\\ &0x=40~~~~~~~~~~~~~~~~~~~~~~~~~\mathrm{Simplificando}\\ &x=\frac{40}0~~~~~~~~~~~~~~~~~~~~~~~~~~\mathrm{Despejando}~x\\ &\textcolor{#ff0080}{\mathrm{Cuidado!}~\frac{ n}0~\mathrm{no~ existe} } \end{align} Por tanto la ecuación no tiene solución.
Ejemplo 8. Ecuaciones fraccionarias. Variables en el denominador. Resolver las siguientes ecuaciones. \begin{align} &\textcolor{#ff0080}{8.1}~~~\frac{3}{2x}+\frac{7}{4x}=\frac{9}{4x}+\frac{4}{12}\\ &\textcolor{#ff0080}{8.2}~~~\frac{6}{x}+\frac{7}{3x}-18=\frac{3}{2x}+\frac{4}{3x}+15\end{align} Solución 8.1: \begin{align} &12x\left(\frac{3}{2x}+\frac{7}{4x}=\frac{9}{4x}+\frac{4}{12}\right)~~~~~12x~\mathrm{es}~m.c.ds.\\ &18+21=27+4x~~~~~~~~~~~~~~~~~~~~~~~~~~ \mathrm{Multiplicando}\\ &39-27=4x~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \mathrm{Trasposición}\\ &12=4x\Longleftrightarrow\frac{12}{4}=x~~~~~~~~~~~~~~~~~~~~~\mathrm{Despejando}~x\\ &3=x~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\mathrm{Simplificando}\end{align} Solución 8.2: \begin{align} &6x\left(\frac{6}{x}+\frac{7}{3x}-18=\frac{3}{2x}+\frac{4}{3x}+15\right)~~~~~~6x~\mathrm{es}~m.c.ds.\\ &36+14-108x=9+8+90x~~~~~~~~~~~~~~~~~~~~\mathrm{Multiplicando}\\ &-108x-90x=9+8-36-14~~~~~~~~~~~~~~~\mathrm{Trasposición}\\ &-198x=-33 ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~ \mathrm{Simplificando}\\ &x=\frac{33}{198} ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \mathrm{Despejando}~ x\\ &x=\frac{1}{6}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \mathrm{Simplificando} \end{align}
Para más contenidos y luego clic en la pestaña del contenido deseado.
Aplicaciones lineales. Modelación.
La modelación matemática consiste en el planteamiento y análisis de fenómenos o situaciones del quehacer científico o la vida cotidiana, mediante modelos matemáticos los cuales permiten describir el comportamiento y/o funcionamiento del ente de estudio.
Muchas situaciones científicas y del diario vivir se expresan mediante el uso de expresiones matemáticas llamadas fórmulas. Para un cuerpo de masa constante \(m\), por la ley de Newton se tiene el modelo \(F=ma\) (fuerza igual a masa por aceleración), para el área de un rectángulo se escribe \(A=wl\), donde \(w\) es el ancho y \(l\) el largo. Ambos modelos dan explicación al fenómeno representado, \(F=ma\), un modelo para la Física y \(A=wl\) es un modelo geométrico.
De modo que, cada modelo matemático es una ecuación, en la cual se debe determinar el valor de una o más variables, partiendo de ciertos datos, pero ¿Cómo resolver una situación matemática sobre ecuaciones? A continuación, se presentan algunas consideraciones importantes, las cuales sirven de gran ayuda al resolver situaciones de modelos matemáticos.
1. Entender el ejercicio, analizar qué se pregunta o qué se pide, cuáles datos se dan. Si es posible realizar un boceto de la situación, esto ayudará a una mejor compresión.
2. Nombrar las variables. Esto es lo que se pregunta o se pide realizar en el ejercicio. Por ejemplo, si un ejercicio expresa ¿Cuál es la altura del edificio? Al nombrar la variable se dice “sea \(h\) la altura del edificio”. Recuerde que las letras son “muda”, puede usar la que desee en vez de \(h\).
3. Construir o escribir el modelo (ecuación o fórmula) partiendo de los datos, plantee las operaciones para el modelo matemático, usando una notación adecuada.
4. Evaluar el modelo. Revise si conoce o no todas las partes (variables y constantes) que involucran el modelo. Si no se tiene alguna, se debe tener una idea de su valor o cómo deducirla a partir de los datos.
5. Realizar operaciones planteadas. Simplifique y resuelva las operaciones planteadas en el modelo (tenga en cuenta el orden operacional). Si hay fracciones, multiplicar toda la expresión por el \(m.c.m.\) de los denominadores simplificará la expresión.
6. Realizar trasposición de términos. Agrupe en un solo miembro todas las variables y en el otro miembro todas las constantes, aplicando el axioma de las igualdades.
7. Despejar la variable. Aplique el axioma de las igualdades, hasta despejar la variable (coeficiente y expoente uno).
8. Escribir y verificar. Escriba y verifique si las respuestas encontradas son lógicamente correctas, para el tipo de variable que está estudiando. Se debe tener en cuenta si la incógnita es una variable discreta (no admite fracción) o una variable continua (admite fracción), además si la misma puede o no ser negativa, así una respuesta de que una persona tiene 3.5 gatos es ilógica, al igual que expresar que un niño tiene menos siete años ¿Puede ser el tiempo negativo?
Problemas de velocidad, tiempo y distancia. En algunas situaciones una partícula se mueve a una rapidez constante \(v\) mal llamada comúnmente velocidad, durante un tiempo \(t\) y recorre una distancia \(d.\) Para tales casos la expresión \(d=vt\) provee la respuesta, según las condiciones.
Para más contenidos y luego clic en la pestaña del contenido deseado.
Ecuaciones lineales con valor absoluto.
Definición de valor absoluto: el valor absoluto de una cantidad \(c\) denotado como \(\left|c\right|\) se define como, $$\left|u\right|=\left\{\begin{array}1 -u~~~\mathrm{si}~ u < 0\\ ~~u~~~\mathrm{si}~ u \geq 0 \end{array}\right.$$ Además, si \(n\) es par en \(\sqrt[n]{u^n}\) entonces \(\sqrt[n]{u^n}=\left|u\right|\).
El valor absoluto de una cantidad \(u\) no considera el signo, y puede interpretarse como la distancia en la recta real desde \(u\) hasta el cero. así por ejemplo se tiene que, $$\left\{\begin{array}{l} \left|-5\right|=-(-5)=5\\ \left|5\right|=5~~~~~~~~~~~~~~\\ \end{array}\right.$$ de donde se infiere que el valor absoluto no considera el signo y por tanto, siempre es positivo.
Algunas propiedades del valor absoluto.
1. \(\left|u\right|\geq0~~~~\) (nunca es negativo).
2. \( \left|u\right|=0\Longleftrightarrow u=0.\)
3. \(\left|uv\right|=\left|u\right|\left|v\right|~~~~\) Valor absoluto de un producto.
4. \(|u/v|=|u|/|v|~~~~\) Valor absoluto de un cociente.
5. \(|u|^n=u^n\) si \(n\) es par.
6. \(\sqrt[n]{u^n}=\left|u\right|\) si \(n\) es par (segunda definición dada).
Aunque existen otras propiedades para el valor absoluto, estás deben esperar a la utilización de resoluciones de desigualdades para ser analizadas.
Para resolver una ecuación líneal con valor absoluto se aplica la definición de valor absoluto y/o propiedades que sean necesarias y se realizan las operaciones indicadas.
Si aun no ha estudiado desigualdades es posible que necesite esperar un poco más para la comprensión de este tema, sin embargo esto no quiere decir que no se puede intentar. La capacidad de aprendizaje es distinta para cada persona.
Ejemplo 1. Resolver \(\left|x-13\right|=5\)
Solución: de la definición de valor absoluto se tiene,
\begin{align}
&-(x-13)=5~~~~~~\mathrm{si}~x-13< 0\\
&x-13=5~~~~~~~~~~~~~~\mathrm{si}~ x-13≥0\\
\end{align}
Resolviendo cada una de estas ecuaciones.
\begin{align}
&-x+13=5\Longrightarrow -x=5-13\Longleftrightarrow x=8\\
&x-13=5\Longleftrightarrow x=18\\
\end{align}
Comprobando las respuestas,
\begin{align}
&\mathrm{si}~x=18 \Longrightarrow \left|18-13\right|=\left|5\right|=5\\
&\mathrm{si}~ x=8 \Longrightarrow \left|8-13\right|=\left|-5\right|=5~\end{align}
Lo que demuestra que ambas soluciones satifacen la ecuación.
Ejemplo 2. Resolver \(\left|25\left(9x-4\right)\right|=125\)
Solución: aplicando la propiedad \(\left|uv\right|=\left|u\right|\left|v\right|\)
se tiene,\(\left|25\right|\left|\left(9x-4\right)\right|=125\) de donde se debe resolver \(25\left|\left(9x-4\right)\right|=125\) y de la definición de valor absoluto resultan las ecuaciones,
\begin{align}
&25(9x-4)=125 ~~~~~~~~~\mathrm{si}~~9x-4\geq0~~~~\boxed{\textcolor{#ff0080}{1}}\\
&25[-(9x-4)]=125~~~~~\mathrm{si}~~9x-4 < 0~~~~~~~~\boxed{\textcolor{#ff0080}{2}}
\end{align}
Resolviendo la ecuación \(\boxed{\textcolor{#ff0080}{1}}\)
\begin{align}
&25(9x-4)=125\\
&225x-100=125\\
&225x=125+100\\
&225x=225\\
&x=\frac{225}{225}\\
&x=1\end{align}
Resolviendo la ecuación \(\boxed{\textcolor{#ff0080}{2}}\)
\begin{align}
&25[-(9x-4)]=125\\
&-9x+4=\frac{125}{25}\\
&-9x+4=5\\
&-9x=5-4\\
&-9x=1\\
&x=-\frac{1}{9}\end{align}
Ejemplo 3. Resolver la ecuación
$$\left|\frac{3x-5}{2x-6}\right|=2$$
Solución: aplicando el valor absoluto de un cociente \(\left|u/v\right|=\left|u\right|/\left|v\right|\) se tiene,
\begin{align}
&\frac{|3x-5|}{|2x-6|}=2\\
&|3x-5|=2|2x-6|\\
\end{align}
Ahora se determinan los intervalos de positividad.
$$
\left|3x-5\right|=\left\{\begin{array}{l}
3x-5 \ \ \ \ {\rm si~} 3x-5≥0 ⟺x≥5/3\\
5-3x \ \ \ \ {\rm si~} 5-3x< 0⟺x< 5/3\end{array}\right.$$
$$\left|2x-6\right|=\left\{\begin{array}{l}
2x-6 \ \ \ \ {\rm si~} 2x-6≥0 ⟺x≥3\\
6-2x \ \ \ \ {\rm si~} 6-2x< 0⟺x< 3\end{array}\right.$$
Estos resultados se ilustran en la figura siguiente,
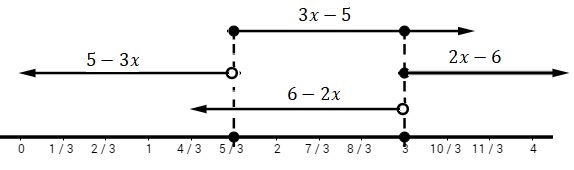
De donde para, \(-\infty< x< 5/3\)
$$\frac{5-3x}{6-2x}=2\Longrightarrow5-3x=2(6-2x)\Longleftrightarrow x=7$$
Para \(5/3\le x< 3\)
$$\frac{3x-5}{6-2x}=2\Longrightarrow3x-5=2(6-2x)\Longleftrightarrow x=17/7$$
Para \(x\geq3\)
$$\frac{3x-5}{2x-6}=2\Longrightarrow3x-5=2(2x-6)\Longleftrightarrow x=7$$
Por lo que se concluye que \(x=17/7\) y \(x=7\) son las soluciones del ejercicio.
Para más contenidos y luego clic en la pestaña del contenido deseado.
Ejemplo 2. Contando monedas. María tiene \($500\) en monedas de \($10\) y \($25\). Si en total tiene \(32\) monedas. Determine analíticamente la cantidad de moneda de cada tipo que tiene.
Ejemplo 3. Dimensiones de un terreno. Un terreno rectangular está rodeado por una cerca de 100m de longitud. Si el largo del terreno es 10m más grande que el ancho. Determine analíticamente las dimensiones del terreno.
Problema de inversión. Una persona nota que al final de los últimos dos años, ha incurrido en gastos extras en el fin del año por \($20\ 000\). Debido a esto decide invertir \($200\ 000\) con la finalidad de recibir los \($20\ 000\) de gastos extras que tiene cada fin de año. Para esto invierte \($40\ 000\) a una tasa de interés simple de un \(8\%\), \($110\ 000\) a un \(11\%\). Determine el porcentaje al que debe invertir el resto del dinero, para obtener los \($20\ 000\) que desea ganar para sus gastos de fin de año.
Problema de mezcla. El nitrato de amonio es un sólido cristalino fabricado en cantidades industriales mayormente como fuente de fertilizantes, pero también utilizado en la industria minera como explosivo. Su composición química es \(NH_4NO_3\). Una gran cantidad de este compuesto almacenado en un puerto fue el causante de la explosión en Beirut, el 4 de agosto del 2020 matando a decenas de personas e hirió a miles, causando pérdidas económicas enormes. Para cierto experimento de un laboratorio escolar se tiene dos litros de nitrato de amonio al \(30\%\). Determine la cantidad de esta mezcla que debe reemplazarse con nitrato de amonio puro, para tener una mezcla al \(75\%.\)
Distancia Santo Domingo - New York. Suponga que en un día con "condiciones normales" un avión comercial vuela con rapidez promedio de \(500\) millas por hora con el viento a favor desde New York a Santo Domingo en tres horas. Si el viaje de regreso es a contra viento y tarda treinta minutos más que el tiempo de ida a igual rapidez. Determinar la distancia de separación de las ciudades y la rapidez del viento.
Ir de compras. Una persona compra un sombrero, una camisa y una chaqueta, por $5500. Si el sombrero costó el doble de la camisa, y la camisa costo el triplo de la chaqueta disminuido en $250. Determinar cuánto pago por cada artículo.
